NURBS кривые для судостроителей.
- Alexander Alexanov
- 14 авг. 2021 г.
- 7 мин. чтения
Обновлено: 19 авг. 2021 г.

Несмотря на то, что NURBS представление кривых и поверхностей давно уже является стандартным инструментом моделирования кривых и поверхностей в судостроении, многие инженеры до сих пор слабо представляют с чем они имеют дело. Попробуем взглянуть на этот инструмент не с математической, а с практической инженерной точки зрения.
Попробуем понять:
- Чем NURBS отличается от обычных сплайнов?
- Какой NURBS лучше?
- Что делать с весами?
- Как определить какая часть кривой изменится при перемещении точки контрольного многоугольника?
- Почему точки контрольного многоугольника не лежат на кривой?
- Что удобнее? Изменять непосредственно кривую или многоугольник?
- Как многоугольник связан с кривой?
Начнем с начала.
NURBS кривая представляет собой набор сегментов параметрических полиномиальных кривых состыкованных между собой ( куда уж тут деться от математики? ). Каждая точка NURBS может быть вычислена в зависимости от параметра U. Думаю, что разбираться что находится внутри Fx, Fy, Fz мы не будем. Примем это как черный ящик.
X = Fx(U)
Y = Fy(U)
Z = Fz(U)
Как видно из этих уравнений, координаты точки на NURBS кривой не зависят друг от друга и зависят только от параметра U. То есть мы можем рисовать кривую любой формы, в том числе с петлями. В этом есть преимущество NURBS перед традиционными математическими сплайнами. Другим преимуществом можно назвать удобство визуализации таких кривых. При вычислении точек с равным шагом по параметру, кривая выглядит плавной и красивой. Недостатком можно назвать то, что при необходимости вычислить точку (или точки) на кривой c фиксированной координатой, потребуется численное решение. Это означает что точка будет вычислена с заданной точностью. Обращаю на это внимание, так как аспект точности важен при передаче данных из одной программы в другую.

Форма любой NURBS кривой определяется следующими параметрами:
Степень и порядок кривой.
NURBS состоит набора полиномиальных сегментов заданной степени. От степени зависит гладкость стыковки сегментов кривой между собой, области изменения NURBS при изменении положения одной контрольной точки и минимальное количество возможных точек контрольного полигона. Минимально возможное количество контрольных точек вычисляется как Степень + 1. Это и называется в разной литературе порядком кривой. Это нужно знать, чтоб встретить во всеоружии разработчиков всяких САПР, которые запугиваю несчастных инженеров подобными терминами. Какая степень лучше? Наверное та, которая выше. Кривая более плавная и красивая. Наверное, это то, что нам нужно?
Ниже я привел пример NURBS степени от 1 до 5, представленный на том же самом наборе контрольных точек. Посмотрите, как влияет степень на форму кривой.
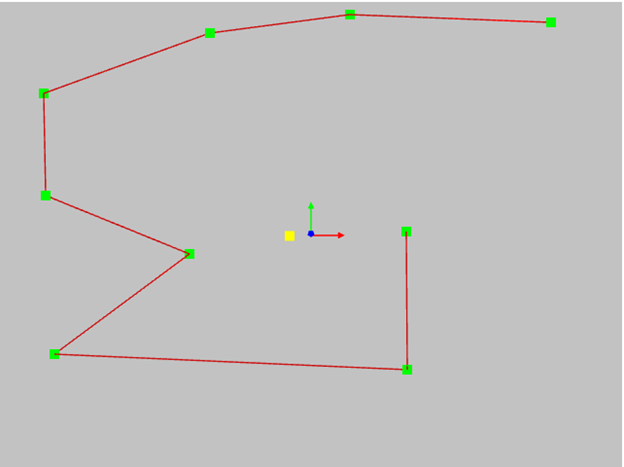
Первая степень – кривая совпадает с контрольным многоугольником. Не интересно. Не стоило даже городить огород. Проще использовать многоугольник.

Вторая степень – кривая уже выглядит как кривая. Обратите внимание на интересное свойство – кривая касается каждой линии контрольного многоугольника. С такой кривой уже можно работать, но – участки такой кривой стыкуются только по касательной. Кривизна такой кривой изменяется скачками от участка к участку. Недостаточная плавность такой кривой будет визуально заметна.

Третья степень – кривая более гладкая. Выполняется непрерывность касательных и кривизны. Эту степень чаще всего используют при проектировании.
Пятая степень. Все лучше и лучше. Выполняется гладкость прoизводных более высокого порядка. Недостатки этих кривых в том, что форма кривой довольно сильно отличается от многоугольника. Другим недостатком можно считать то, что при изменении одной контрольной точки изменяется значительная часть кривой. Так что любителям перфекционизма в проектировании судов скажу – не удивляйтесь, если при изменении линии в районе бульба изменится половина носовой оконечности. Контролировать такую кривую значительно сложнее.
Так что при выборе степени NURBS следует прислушаться к здравому смыслу. Как дополнительный аргумент приведу в пример функцию синуса или косинуса как бесконечно гладких кривых с точки зрения математики. Однако их никто не использует для проектирования судов.
Контрольный многоугольник.
Наконец-то мы пришли к одному из самых важных свойств NURBS – контрольному многоугольнику кривой. Собственно говоря, это то, за что этот класс кривых и поверхностей называют скульптурными. В отличие от сплайнов, где кривая проходит через набор точек, форма NURBS кривых определяется формой многоугольника, где кривая проходит только через начальную и конечную точки многоугольника. Во всех остальных случаях форма кривой лишь повторяет форму многоугольника, но не проходит через все его точки. Это было хорошо видно на примере изменения степени кривой. Сплайн проще, скажете вы, сплайн проходит через все заданные точки. Сплайном легче управлять. На самом деле это не играет существенной роли при проектировании, а условие прохождения линии через заданную точку используется очень редко. Вместе с тем NURBS имеет гораздо больше полезных свойств, а интерактивное изменение формы кривой при изменении точек контрольного многоугольника ничуть не сложнее, чем изменение положения точки сплайна.
Итак, форма NURBS кривой определяется формой контрольного многоугольника. Что надо знать при работе с контрольным многоугольником:
- Кривая начинается и заканчивается в конечных точках контрольного многоугольника.
- Углы наклона кривой в конечных точках совпадают с углами наклона отрезков многоугольника в конечных точках.

- Степень прилегания кривой в конечных точках зависит от длины соответствующего отрезка. Как это показано на картинке ниже.

- Для кривых второй степени кривая касается каждого отрезка

- в случае кривых третьей степени кривая касается многоугольника, если три последовательные вершины лежат на одной прямой. В этом случае точка касания совпадает со средней точкой.
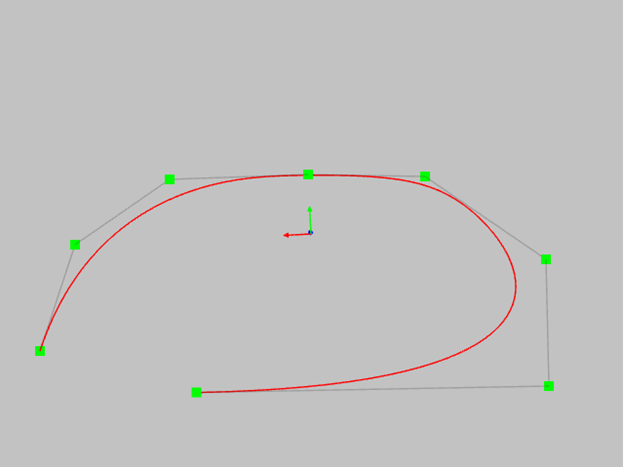
- если для кривой третьей степени четыре точки лежат на одной прямой, участок кривой будет совпадать со средним отрезком многоугольника и будет представлять собой математически точную прямую. Больше точек на одной прямой – больше прямолинейная область нашей кривой.

Попробуйте сделать то же самое с классическим сплайном. С большой уверенностью могу сказать, что в этой ситуации классический сплайн будет осциллировать вокруг требуемой прямой.
Следующий пример показывает, как в этом случае ведет себя кривая пятой степени. Что получить касательную в точке нужно, чтоб пять точек многоугольника были на одной прямой. Если требуется строго прямолинейный участок, точек должно быть еще больше. Одним словом, чем выше степень, тем сложнее контролировать форму.

- рассмотрим еще одно, на мой взгляд потрясающее свойство NURBS кривых – это свойство выпуклой оболочки. Если многоугольник выпуклый – кривая не будет иметь точек перегиба. Для невыпуклого многоугольника кривая всегда будет иметь перегибы.

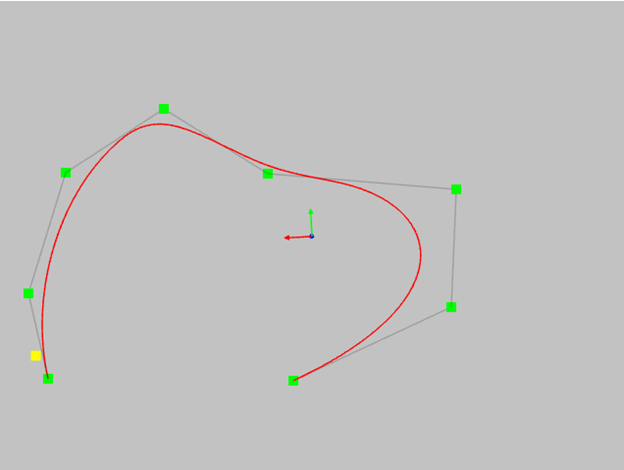
Это свойство позволяет контролировать форму кривой даже без использования графика кривизны.
- еще одно очень важное свойство это локальность изменения формы кривой. Если изменить положение одной контрольной точки, то изменится только часть кривой. Область изменения кривой зависит от степени NURBS.
Область изменения для кривой второй степени.

Область изменения для кривой третьей степени.
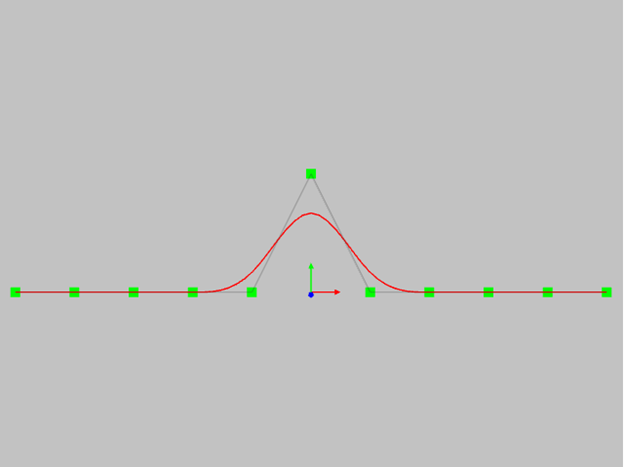
Область изменения для кривой пятой степени. Обратите внимание на то, что область изменения кривой в этом случае очень большая.

Суммируя все, что мы здесь узнали о контрольном многоугольнике:
- Основное средство управления формой кривой.
- Позволяет моделировать кривую практически любой формы, даже с прямолинейными участками.
- Позволяет локально изменять форму кривой.
- Плавность кривой зависит от степени кривой, но, как и везде, за все надо платить. Плавная кривая высокой степени сложнее в управлении.
Добавлю только то, что при моделировании кривых старайтесь равномерно распределять точки контрольного многоугольника вдоль кривой. ”Kрасивый” контрольный многоугольник определяет плавную и качественную кривую.
Весовые коэффициенты.
В литературе, как и в руководствах различных 3D программ часто используются два термина B-Spline и NURBS. В чем различие? NURBS отличается от B-Spline только тем, что точки контрольного многоугольника NURBS кроме координат X,Y,Z, имеют дополнительный параметр, который называется весом. Смысл этого параметра в том, что дизайнер имеет возможность определять какая из точек контрольного многоугольника может сильнее влиять на форму кривой. Если веса у всех точек одинаковы (что чаще всего и бывает), то это и есть B-Spline. Чаще всего вес равен единице. Если значение веса в какой-либо точке равно нулю, это говорит о том, что данная точка не влияет на форму кривой. Математически красиво, но практически непонятно. Если точка имеет вес больше 1, например 2, то кривая как бы притягивается к этой точке. Часто веса используются внутренними функциями какой-либо системы моделирования для узко специализированных нужд. Например, используя веса можно задать математически точную окружность. При использовании B-Spline это невозможно. Если задать вес очень большим, например 10, то кривая будет проходить очень близко к точке. Визуально это может выглядеть как точка слома на линии. Но это только визуально. Линия не будет математически точно совпадать с точкой.
Так выглядит кривая с нулевым значением веса в центральной точке.

Вес равен 1

Вес равен 2

Вес равен 10

Обращаю ваше внимание на то, что в отличие от изменения степени кривой, изменение веса в точке не приводит к изменению области модификации кривой. Это то, что нужно знать о весах в точках контрольного многоугольника.
Узловой вектор.
NURBS кривая представляет собой набор сегментов полиномиальных кривых. Благодаря этому мы и имеем такие замечательные свойства, как локальность модификации кривой и возможность спрямления части кривой. Форма каждого из этих сегментов (их еще называют span), зависит от нескольких точек контрольного многоугольника. Каждый сегмент начинается и заканчивается в узлах – точках на кривой, представляющих собой границы сегмента. Узлы определяются значениями параметра кривой. Число узлов определяется ка число точек контрольного многоугольника + порядок кривой. Расположение узлов определяется узловым вектором. Как правило узловой вектор используется для внутренних манипуляций в программах 3D моделирования. Изменять узловой вектор для изменения формы кривой практически нереально. Для практической работы по моделированию кривых наиболее важно иметь равномерное распределение узлов и сегментов кривой по параметру. В этом случае изменение положения контрольных точек кривой будет наиболее предсказуемо.
На этом примере показана кривая третьей степени с многоугольником из 5-ти контрольных точек. В этом случае кривая имеет два сегмента. Желтая точка показывает границу между сегментами.

Узловой вектор будет выглядеть так: 0,0,0,0, 0.5,1,1,1,1 – значение 0.5 как раз и соответствует узловой точке. Чем узловые точки отличаются от любых других точек на кривой? Узловые точки помогают нам контролировать форму кривой. На примере ниже показано положение узла (желтая точка), в котором начинается криволинейная область кривой. Сегменты кривых могут быть прямолинейными или криволинейными только в переделах одного сегмента. Поэтому, как бы вы этого ни хотели, только в узловой точке кривая может переходить в математически точную прямую. Как пример можно привести линию палубы, переходящую в плоский борт. Думаю, что на любой судоверфи возникнут вопросы к конструктору, если плоский борт вдруг станет немного неплоским. См. ниже.

Какую бы программу для моделирования линий и поверхностей вы не использовали, каждая из них использует NURBS. Способов управления формой линий может быть много. Некоторые программы используют касательные в конечных точках и узлы, как средство редактирования кривой. Некоторые позволяют модифицировать любую точку на кривой. В итоге все они всё равно сводятся к тем свойствам NURBS о которых я рассказал выше.
NURBS это как музыкальный инструмент и от правильной настройки этого инструмента существенно зависит конечный результат. Иллюстрации, которые вы видите в этой статье я сделал в интернете на сайте "nurbscalculator.in" Это простой и удобный NURBS онлайн калькулятор. Вы можете сами попробовать различные варианты параметров кривой и оценить насколько это приемлемо для вас.




Очень даже познавательная статья. В ShapeMaker есть линии: безье, сплайн, в-сплайн. Это и есть NURBS кривые? А как задавать вес каждой точки, чтобы управлять такой кривой?